Zusammenfassung: Harmonische Schwingungen

Federpendel und Fadenpendel, letzteres für kleine Auslenkungen, sind zwei bekannte Beispiele für sog. harmonische Schwingungen. Harmonische Schwingungen sind dadurch gekennzeichnet, dass die rücktreibende Kraft $F$ proportional zur Elongation $s$ ist, also $F \sim s$, oder als Gleichung:

$\fbox{$F=-c \cdot s$}$.

Gleichwertig damit ist, dass das zeitliche Schwingungsverhalten beschrieben wird durch eine Sinusfunktion:

$\fbox{$s(t)=s_0 \cdot sin(\omega t)$}$.

Hieraus lässt sich ableiten, dass die Schwingungsdauer $T$ unabhängig von der Amplitude der Schwingung ist:

$\fbox{$T$ unabhängig von $s_0$}$.

Zu den harmonischen Oszillatoren (mechanischer Natur) gehören:
➡ Federpendel
➡ Fadenpendel (in guter Näherung bei kleinen Auslenkungen)
➡ Wassersäule in einem U-Rohr (trotz erheblicher Reibung)
➡ in Wasser eintauchendes unten beschwertes Reagenzglas
➡ Blattfeder
➡ Saite
...

Beispiele für nichtharmonische Oszillatoren (mechanischer Natur) sind:
➡ Fadenpendel (bei größeren Auslenkungen)
➡ rollender Wagen auf einer Knickbahn
➡ in Wasser eintauchender unten beschwerter Trichter
➡ hüpfende Kugel auf harter Unterlage
...

Tipp

Geben Sie eine begründete plausible Begründung dafür an, warum harmonische Schwingungen als solche bezeichnet werden.

Beschreiben Sie, woran man bei den kurzen Videos zur schwingenden Wassersäule und zum tauchenden Reagenzglas (s. o.) die harmonische Schwingung, bei der hüpfenden Kugel die anharmonische Schwingung "sehend" bzw. "hörend" erkennen kann - also ohne erst irgendwelche Messwerte aufzunehmen.

Denken Sie daran, wie sich eine schwingende Saite und auch eine schwingende Luftsäule anhören würden, wenn sie zu den nichtharmonischen Schwingern gehören würden.

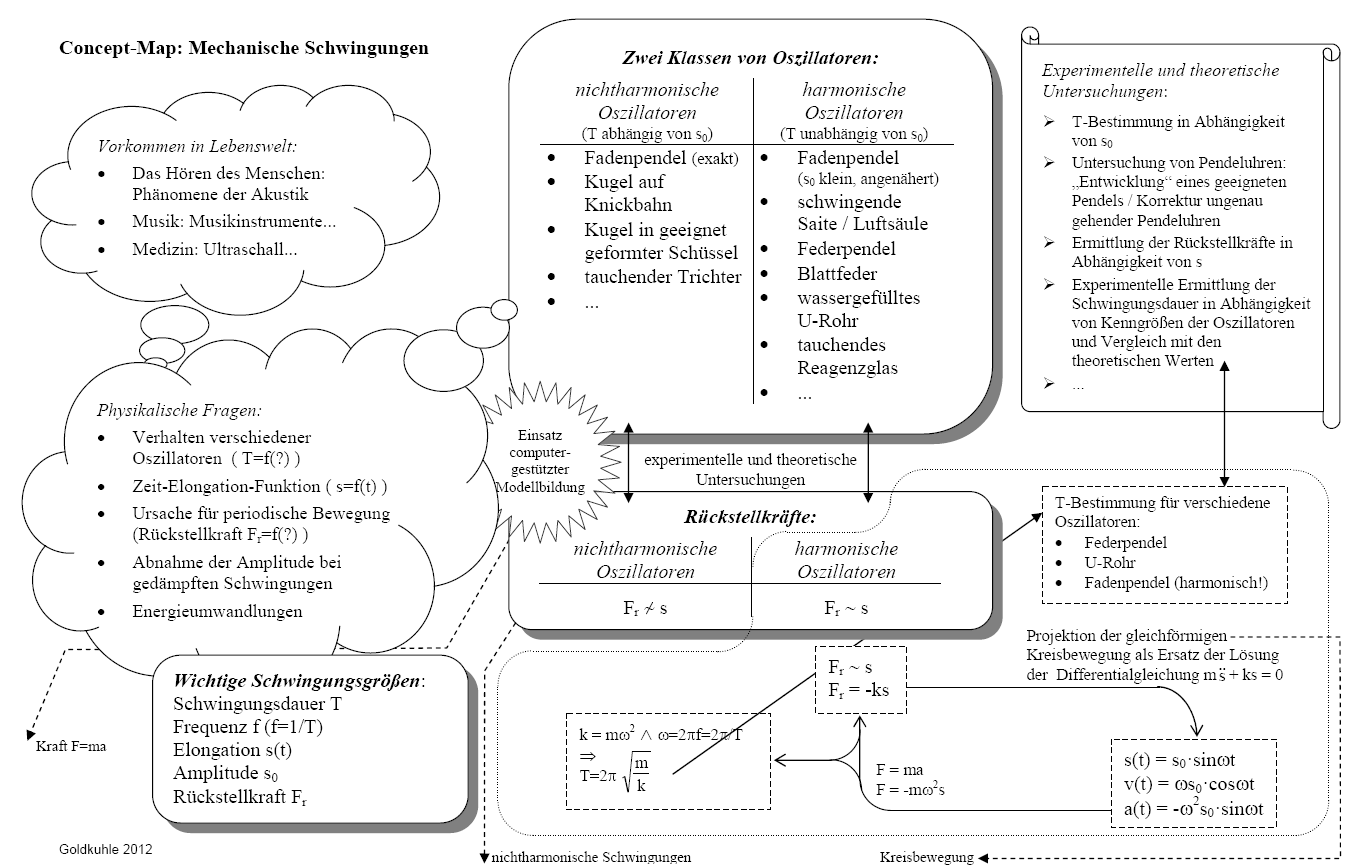
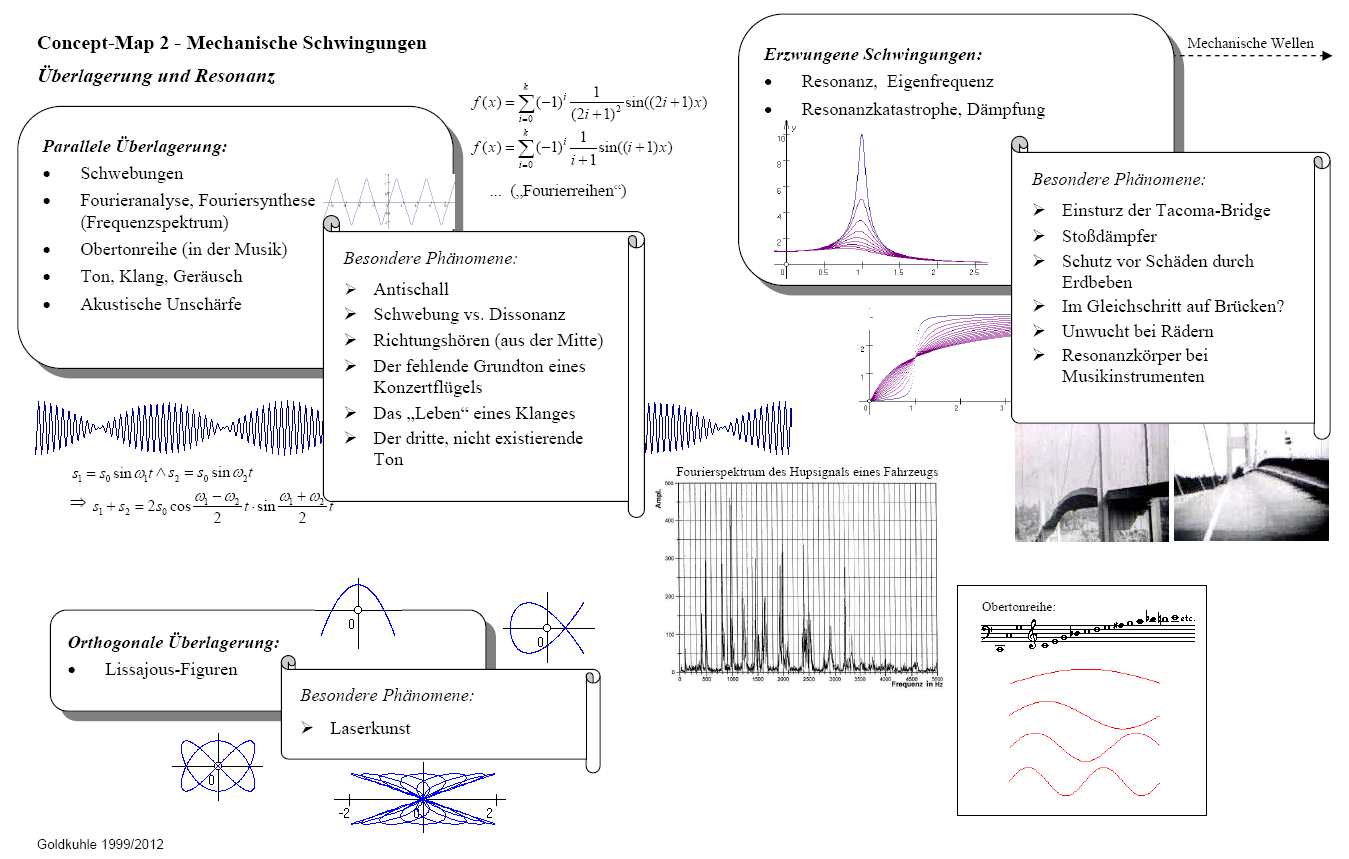
Die beiden durch Anklicken nacheinander einblendbaren Übersichten zeigen zusammenfassende Darstellungen von Phänomenen, deren Zusammenhängen und auch theoretischen Erläuterungen zu mechanischen freien und erzwungenen Schwingungen. Sie eignen sich zur Strukturierung und Wiederholung des erarbeiteten Wissens über Schwingungen.