Zentrale Experimente Physik GOSt
Startseite → Mechanische freie und erzwungene Schwingungen → Aufnahme von Resonanzkurven mit dem IBE
Aufnahme von Resonanzkurven mit dem IBE
Laser-Bewegungssensor
Monitor (vergrößerbar)
Skala (vergrößerbar)
Schraubenfeder
Wirbelstrombremse
Pendelkörper
Diagrammachsen
skalierbar
Netzgerät für
Wirbelstrom-bremse
Wirbelstrom-bremse
Exzenter mit Nullstellung
Motor für Exzenter
Netzgerät für Einstellung der Exzenterfrequenz
Für die Durchführung der Messungen kann man im IBE mittels Motor und Exzenter die (obere) Aufhängung der Schraubenfeder mit der zu wählenden Frequenz des Erregers auf- und abbewegen. Die Amplitude des Erregers ist dabei durch den Aufbau des Exzenters fest vorgegeben. Die Frequenz des Erregers kann über den Drehknopf am Netzgerät für den Motor nach dessen Einschalten variiert werden.
Mittels Laser-Bewegungssensor registriert man den $s_{Err}(t)$-Verlauf des Erregers, den $s_{Res}(t)$-Verlauf des an der Schraubenfeder hängenden Pendelkörpers bestimmt man über einen Bewegungsmesswandler. Beide Verläufe können am Monitor gleichzeitig dargestellt werden.
Hinsichtlich einer wünschenswerten Genauigkeit beim Ablesen von Daten aus den Messkurven sollten Sie unbedingt daran denken, die Achsenskalierungen entsprechend den Erfordernissen beim Ablesen sinnvoll zu wählen bzw. einzustellen (siehe Erläuterungen beim Einblenden des "+"-Zeichens unten rechts unter dem IBE).
Wie auf der vorherigen Seite bereits qualitativ festgestellt, hängt die Amplitude des Resonators sehr stark davon ab, mit welcher Frequenz er durch den Erreger angeregt wird. Folgende drei Fälle konnten unterschieden werden:
- Liegt die Erregerfrequenz in der Nähe der Eigenfrequenz des Resonators, also der Frequenz, mit der er als freier Oszillator schwingen würde, dann ist dessen Amplitude in Abhängigkeit von der konkreten Dämpfung groß. Der Versatz zwischen Erregerkurve und Resonatorkurve liegt bei 90°.
- Schwingt der Erreger viel schneller als mit dieser Resonator-Eigenfrequenz, gehen die Amplituden des Resonators gegen null. Der Resonator schwingt genau gegensinnig zum Erreger.
- Schwingt der Erreger vergleichsweise sehr langsam, stimmen Resonator und Erregeramplitude fast genau überein und haben auch keinen zeitlichen Versatz zueinander.
Auf dieser Seite werden die Aussagen hinsichtlich der Amplitude und Phasenverschiebung durch Messungen quantifiziert: Es ergeben sich die sogenannten Resonanzkurven für das Amplitudenverhältnis $\frac{s_{0,Res}}{s_{0,Err}}$ sowie die Kurven für die Phasenverschiebung $Δφ$ zwischen den $s(t)$-Kurven.
Um das Verfahren kennenzulernen, werden zunächst für eine ausgewählte, fest eingestellte Dämpfung (Stromstärke durch Wirbelstrombremse $I=0,80A$) die Amplituden des Resonators und seine Phasenverschiebungen exemplarisch aufgenommen, wenn die Erregerfrequenz alle im IBE einstellbaren Werte durchläuft.
Bisher wurden das Amplitudenverhältnis $\frac{s_{0,Res}}{s_{0,Err}}$ und die Phasenverschiebung $Δφ$ für die feste Dämpfung mit $I=0,80A$ ermittelt. Im weiteren Verlauf soll die Abhängigkeit dieser beiden Größen von der Stärke der Dämpfung untersucht werden.
Mit Hilfe des IBE können die zu jeder einstellbaren Dämpfung sich ergebenden Amplituden des Resonators $s_{0,Res}$ gemessen werden. Die jeweilige Phasenverschiebung $Δφ$ gegenüber der Erregerschwingung wird im Monitorbild dabei direkt angegeben und kann also solche übernommen werden.
Wegen der recht umfangreichen Messung ist es sinnvoll, sich mit Hilfe einer Tabellenkalkulation eine externe Tabelle zur Aufnahme dieser Messwerte vorzubereiten: Diese Tabelle kann derart gestaltet werden, dass in einer Spalte zunächst die Positionen des Drehreglers für die Erregerfrequenz und in der Spalte daneben die zugehörigen Erregerfrequenzen $f_{Err}$ festgehalten werden.
Da üblicherweise die beiden Resonanzkurven das Verhältnis $\frac{s_{0,Res}}{s_{0,Err}}$ sowie die Phasenverschiebung $Δφ$ in Abhängigkeit von $\frac{f_{Err}}{f_{0,Res}}$ darstellen, könnte die Tabelle etwa folgendermaßen aussehen:
Sollten Sie Schwierigkeiten bei der Anlage einer eigenen Tabelle haben, können Sie sich nebenstehend eine (weitgehend leere) Auswertungstabelle (Excel) herunterladen.
Bestimmen Sie zunächst, noch ohne den Exzenter als Erreger einzuschalten, die Eigenfrequenz $f_{0,Res}$ des Resonators (Federpendel).
Da die Eigenfrequenz mit zunehmender Dämpfung etwas zunimmt, sollten Sie hier die kleinstmögliche Dämpfung auswählen, also die Wirbelstrombremse gänzlich abschalten. Alle späteren Auswertungen beziehen sich dann auf diese Frequenz als $f_{0,Res}$.
Bestimmen Sie die Amplitude $s_{0,Err}$ der Erregerschwingung.
Sie kann (hier technisch bedingt) nicht verändert werden und bleibt daher für alle Messungen konstant.
Tipp: Zur Aufnahme des $s_{Err}(t)$-Diagramms des Erregers können Sie den Resonator einfach ganz oben oder ganz unten festhalten, wenn Sie das (nicht abschaltbare) $s_{Res}(t)$-Diagramm irritieren sollte.
Nehmen Sie hinreichend viele Messwerte auf und lassen Sie sich Ihre gemessenen Werte in zwei Diagrammen darstellen, bei denen auf der Rechtsachse jeweils das Verhältnis $\frac{f_{Err}}{f_{0,Res}}$ aufgetragen ist. In Diagramm 1 sollte das Frequenzverhältnis $\frac{s_{0,Res}}{s_{0,Err}}$ auf der Hochachse aufgetragen sein, in Diagramm 2 die Phasenverschiebung $Δφ$.
Beschreiben Sie den Verlauf der Kurven in Diagramm 1 insbesondere hinsichtlich der Amplituden bei unterschiedlichen Dämpfungen und erläutern Sie damit auch den Begriff Resonanzkatastrophe.
Beschreiben Sie Gemeinsamkeiten und Unterschiede aller Kurven in Diagramm 2.
Bestimmen Sie anhand des IBE das Verhältnis $\frac{s_{0,Res}}{s_{0,Err}}$für alle Erregerfrequenzen bei fest vorgegebener Dämpfung mit $I=0,80A$ in Abhängigkeit vom Verhältnis $\frac{f_{Err}}{f_{0,Res}}$ und tragen Sie die Werte in die nachfolgende Tabelle ein.
Achtung: Dezimalpunkt statt -komma eingeben.
Taschenrechner ein-/ausblenden
7
8
9
4
5
6
1
2
3
.
0
/
*
^
-
+
=
AC
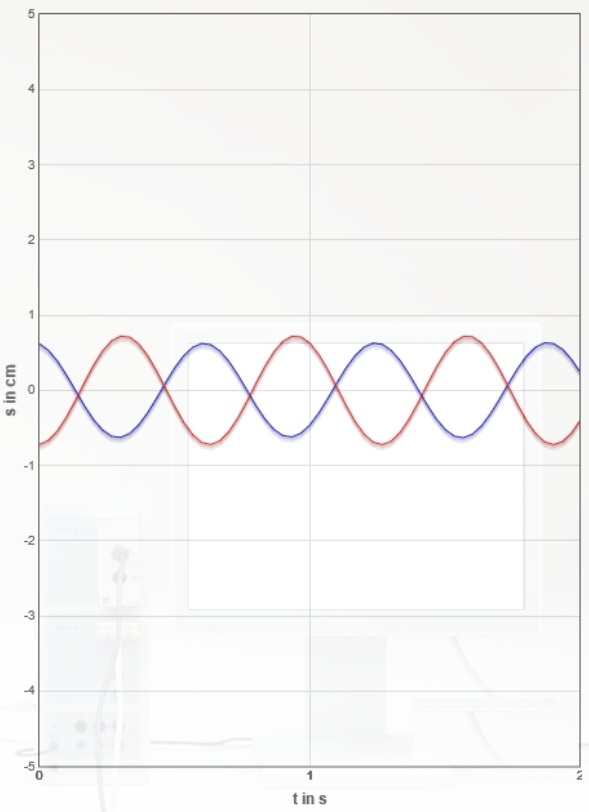
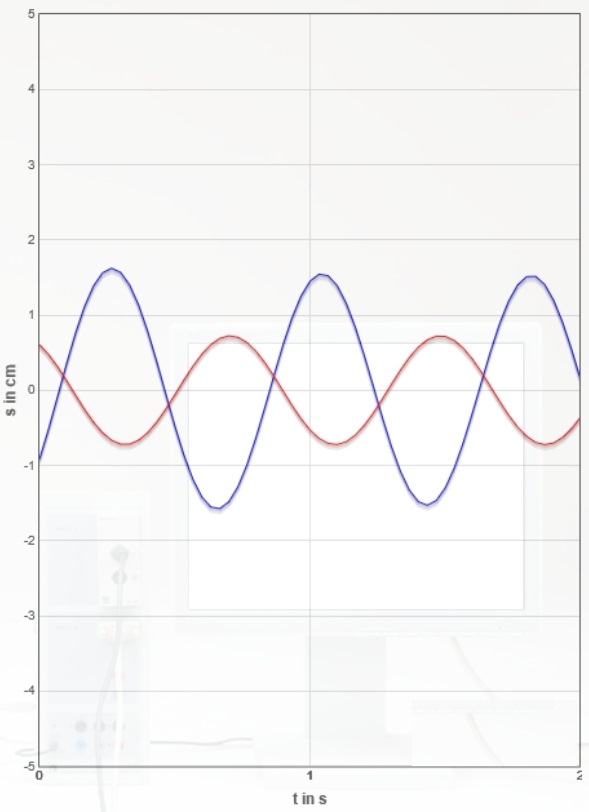
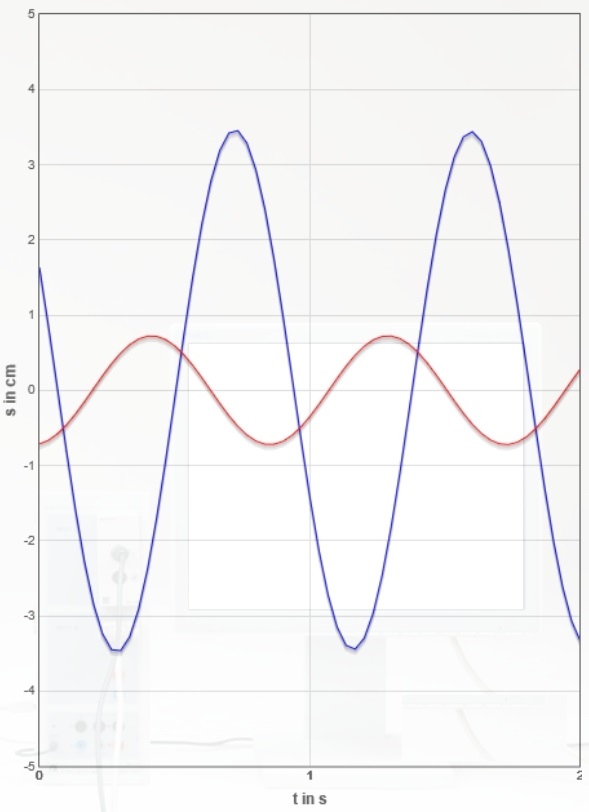
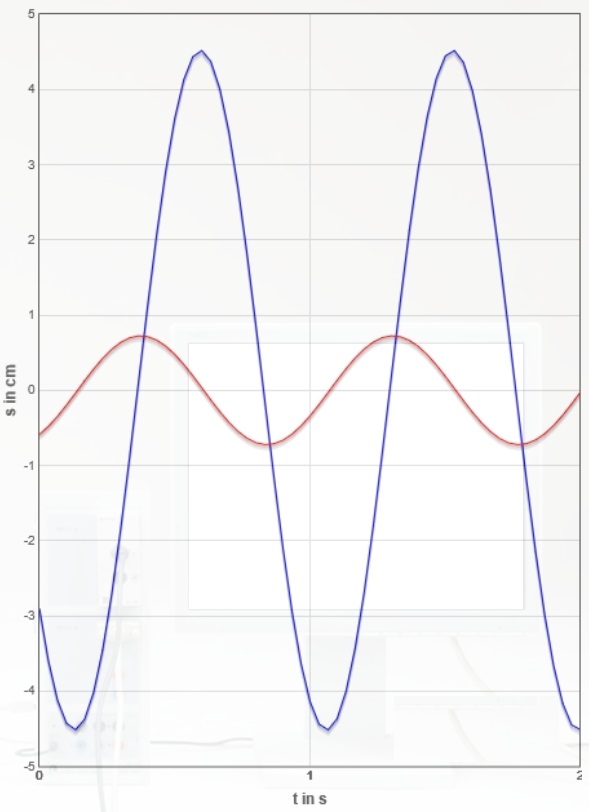
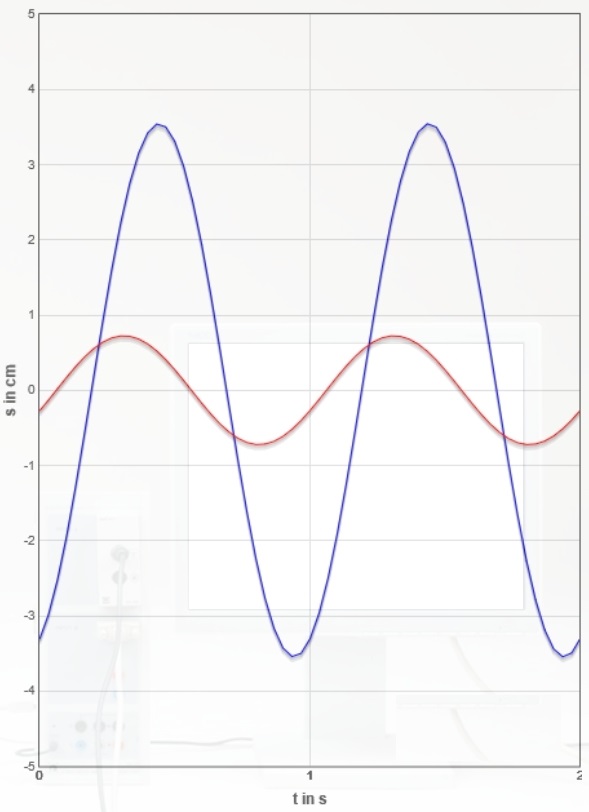
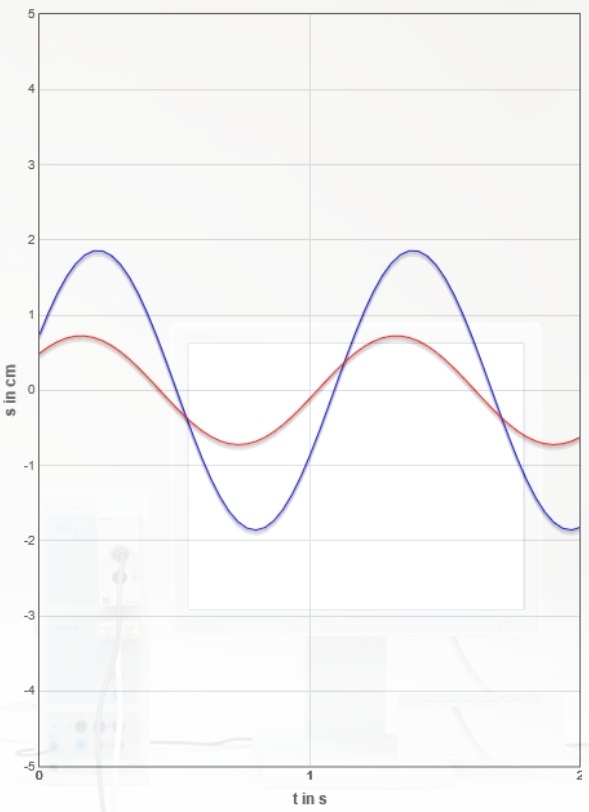
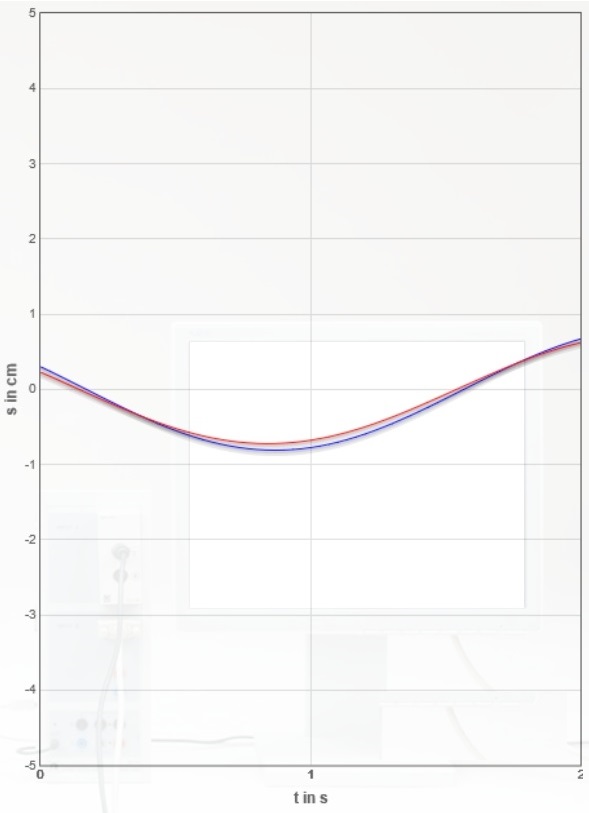
Nachfolgend sind für die oben genannte Dämpfungseinstellung ($I=0,80A$) insgesamt sieben Erreger- und Resonator-Zeitdiagramme Bildschirmfotos der Monitordiagramme erstellt worden (zum Weiterschalten Grafik anklicken).
Bestimmen Sie für alle sieben Diagramme die Phasenverschiebung $Δφ$ zwischen Erreger- und Resonatorkurve in Abhängigkeit vom Verhältnis $\frac{f_{Err}}{f_{0,Res}}$ durch Ausmessen der Kurven.
Achtung: Dezimalpunkt statt -komma eingeben.
Taschenrechner ein-/ausblenden
7
8
9
4
5
6
1
2
3
.
0
/
*
^
-
+
=
AC
Beschreiben Sie stichwortartig Ihr Vorgehen bei der Ermittlung der Phasenverschiebung zwischen den Kurven.
Hinweis: Die im IBE realisierte automatische Errechnung der Phasenverschiebung basiert auf Bestimmung der Zeitdifferenz Δt zwischen (steigendem) Nulldurchgang der Erregerschwingung und dem darauf folgendem (steigenden) Nulldurchgang der Pendelschwingung.