
| Hergestellt mit tet.folio | © 2015 AG Didaktik der Physik | Freie Universität Berlin | CC BY-SA 3.0 |
physik
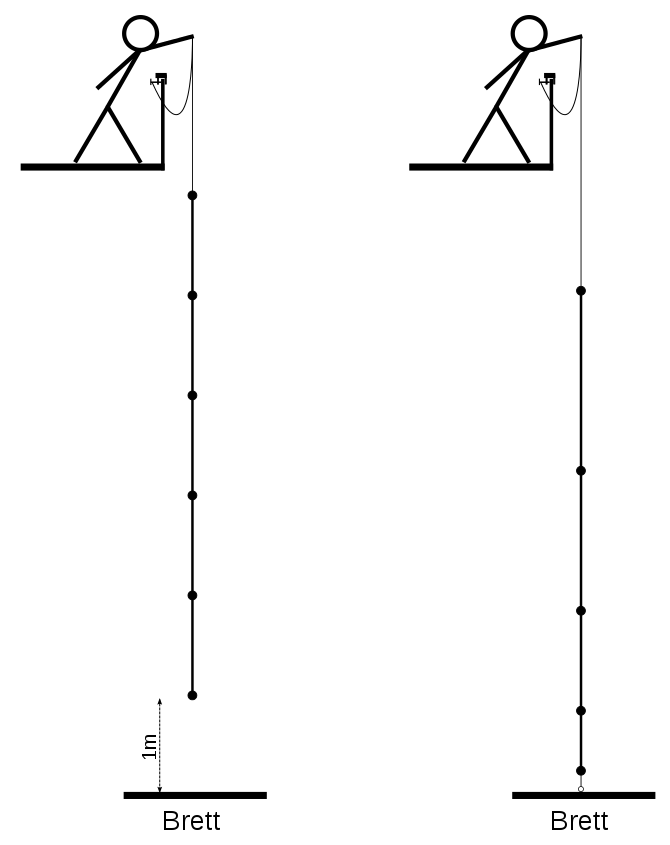
Die Fallschnur
Die Fallschnur demonstriert, dass der freie Fall aus geringen Höhen eine gleichmäßig beschleunigte Bewegung ist, also dem Weg-Zeit-Gesetz der Form
genügt.
Ist der Abstand der Gewichte konstant, so werden die Zeitintervalle zwischen dem Auftreffen aufeinanderfolgender Gewichte immer kleiner:
Um konstante Zeitintervalle zu erreichen, müssen größer werdende Abstände zwischen den Gewichten verwendet werden:
Teste mit der Stoppuhr, ob die Zeitintervalle bei der Fallschnur mit linear zunehmendem Abstand der Gewichte konstant sind.
_
1 An der linken Fallschnur sind Gewichte mit einem konstanten Abstand von 1 m befestigt. Rechts vergrößert sich der Ab-stand von $s_{1}$= 0,2 m um jeweils 0,4 m.
2 Video der AG Vorlesung zur Demonstration des Weg-Zeit-Gesetzes beim freien Fall mit Fallschnüren. Um die Zeitintervalle bequem messen zu können, wird die Fallbewegung in 16-facher Zeitlupe gezeigt.









































$$ \sqrt{n^2 \cdot s} \propto n \cdot t \quad \rightarrow \quad \Delta s_n = (2n-1)s_1 \quad \text{und} \quad \Delta t_n = \text{const}$$
$${\sqrt{n\cdot s_{1}}}\propto {\sqrt{n}}\cdot t_{1}\quad \rightarrow \quad \Delta s_{n}={\text{const}}\quad {\text{und}}\quad \Delta t_{n}=({\sqrt{n}}-{\sqrt{n-1}})t_{1}$$
$$s={\frac{1}{2}}gt^{2}\quad {\text{bzw.}}\quad {\sqrt{s}}\propto t$$
Name: ___________________________________________________ Datum: _________________
