Zentripetalbeschleunigung und Zentripetalkraft

Gemäß den Newton'schen Grundsätzen bewegt sich ein Körper mit konstanter Geschwindigkeit $\vec v$, solange keine Kraft $\vec F$ auf ihn einwirkt. Eine Geschwindigkeit $\vec v$ ist dann nicht mehr konstant, wenn sich deren Betrag, deren Richtung oder beides gleichzeitig verändert. Für einen sich auf einer Kreisbahn bewegenden Körper heißt das, dass diese Bewegung ohne permanente Krafteinwirkung nicht stattfinden kann: Bei einer gleichförmigen Kreisbewegung muss diese Kraft dazu dienen, allein die Richtung der Geschwindigkeit - bei Beibehaltung ihres Betrags - zu ändern. Die sich daraus ergebende Beschleunigung $\vec a_Z=\frac{\vec{Δv}}{Δt}$ wird im Folgenden berechnet.

Eine ähnliche Herleitung der Formel für die Zentralbeschleunigung $a_Z$ basiert auf der Idee eines vollständigen Umlaufs des Punktes $P$ auf dem Kreis, wobei man diesen Kreis in $n$ gleiche Teile unterteilt denkt.

Da allgemein Kraft $\vec{F}$ und Beschleunigung $\vec{a}$ über die Grundgleichung der Mechanik $\vec{F}=m\cdot \vec{a}$ miteinander verbunden sind, folgt für den Fall des Vorliegens einer Zentralbeschleunigung zunächst betragsmäßig: $F_Z=\frac{m\cdot v^2}{r}$ und $F_Z=m\cdot r \cdot \omega^2$.
Die Ergänzung zu einer vektoriellen Darstellung ist im Fall der zweiten Gleichung einfach: $\vec F$ ist immer zum Zentrum der Kreisbewegung hin, also entgegengesetzt zu $\vec r$ gerichtet, daher folgt sofort: $\vec{F_Z}=-m\cdot \omega^2 \cdot \vec r$.
Für die erstgenannte Gleichung verwendet man zur Einführung der Richtung folgenden "Trick": Man multipliziert den rechten Term mit einer Größe, die lediglich eine Richtung, aber keinen weiteren Beitrag zu Betrag und Einheit liefert. Das ist tatsächlich realisierbar! So liefert der Term $\frac{\vec r}{r}$ einen Vektor ohne Einheit und mit dem Betrag $1$. Damit lässt sich $\vec {F_Z}$ vektoriell darstellen durch: $\vec{F_Z}=-m\cdot \frac{v^2}{r} \cdot \frac{\vec r}{r}=-m\cdot \frac{v^2}{r^2} \cdot \vec r$, das Minuszeichen steht hier wiederum, weil $\vec {F_Z}$ und $\vec r$ entgegengesetzt zueinander gerichtet sind.

Tipp 1

Tipp 3

Lösung

Tipp 2

Bestimmen Sie $v=\frac{Δs}{Δt}$ für einen vollständigen Umlauf von $P$.

Vergleichen Sie beide Ergebnisse miteinander und bilden Sie einen geeigneten Quotienten.

Bestimmen Sie $a_Z=\frac{Δv}{Δt}$ bei einem vollständigen Umlauf.

Tipps

Leiten Sie anhand eines vollständigen Umlaufs von $P$ auf dem Kreis die Gleichung für die Zentralbeschleunigung $a_Z=\frac{v^2}{r}$ (bzw. auch $a_Z=r\cdot \omega^2$) her.

Aktivieren Sie das Kontrollkästchen zum Einblenden des Geschwindigkeitsvektor im Punkt $P$.
Begründen Sie, warum die Winkel $\alpha_1$ und $\alpha_2$ gleich groß sind.

Ein Körper im Punkt $P$ war eine Zeitspanne $Δt$ zuvor im Punkt $Q$.
Beschreiben Sie, wie sich seine Geschwindigkeit $\vec {v_P}$ in dieser Zeit verändert hat.

Variieren Sie die Zeitspanne $Δt$ und begründen Sie, dass bei kleiner werdender Zeitspanne die Länge des (kleinen) Kreisbogens $Δs$ mit der der Strecke $\overline{PQ}$ immer besser übereinstimmt.

Tipp 1

Tipp 3

Lösung

Tipp 2

Nutzen Sie aus, dass die beiden genannten Dreiecke ähnlich zueinander sind.

Verwenden Sie die vier Größen $r$, $v$, $Δv$ und $Δs$ mit der o. g. Näherung,

In ähnlichen Figuren sind die Verhältnisse einander entsprechender Strecken gleich.

Tipps

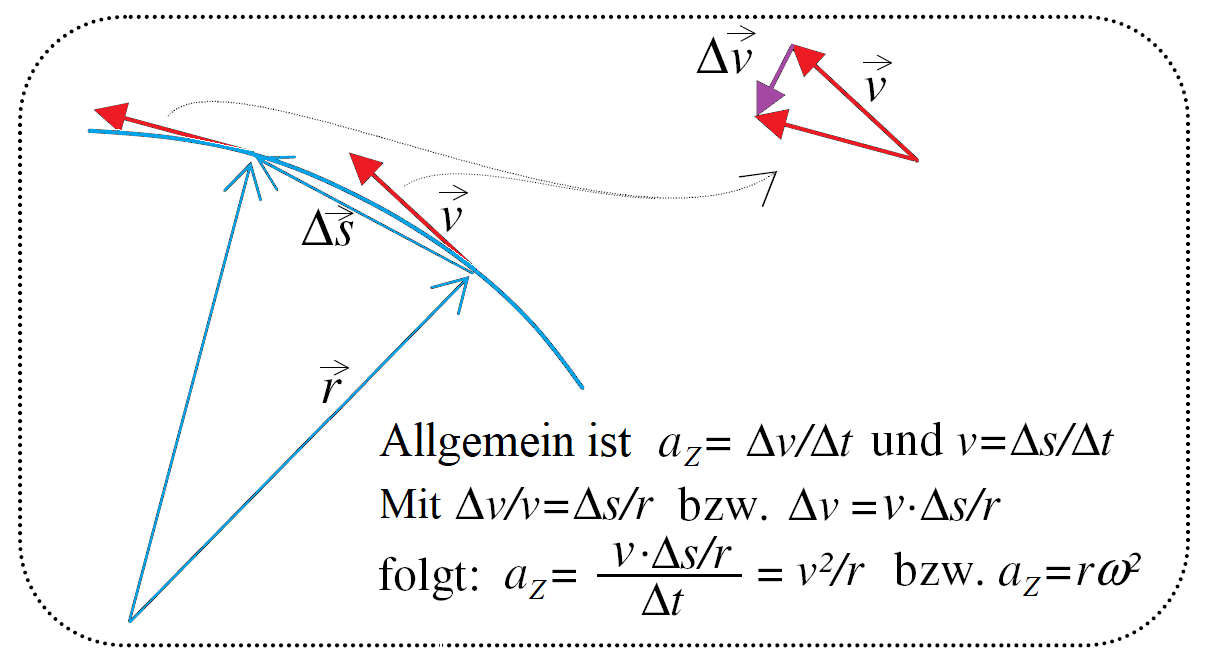
Blenden Sie nun den Vektor $\vec {Δv}$ ein. Leiten Sie anhand der beiden Dreiecke MQP und M'Q'P' sowie der beiden allgemeinen Definitionsgleichungen $v=\frac{Δs}{Δt}$ bzw. $a=\frac{Δv}{Δt}$ für die Beträge von Geschwindigkeit bzw. Beschleunigung die Gleichung für die Zentralbeschleunigung $a_Z$ her: $a_Z=\frac{v^2}{r}$ bzw. $a_Z=r\cdot \omega^2$.

In der folgenden Animation läuft ein Punkt P auf einem Kreis mit einstellbarem Radius mit einer einstellbaren Geschwindigkeit um (P kann auch per Hand bewegt werden).
Die Geschwindigkeitsvektoren in $P$ und $Q$ werden, ausgehend von einem gemeinsamen Punkt $M'$ rechts neben dem blauen Unlaufkreis, eigenblendet. Blenden Sie dabei den Vektor $\vec {Δv}$ zunächst noch nicht ein.

In der folgenden Animation können Sie die Anzahl $n$ der gleich großen Kreisteile voreinstellen.
Es können danach alle Geschwindigkeitsvektoren sowie auch die Änderungen der Geschwindigkeiten von Punkt zu Punkt angezeigt werden.