Laden Sie die rechts stehende weitere Excel-Datei herunter. Sie gibt in der Form eines Quadrats mit 10.000 Zellen durch deren Einfärbung den Zerfallprozess einer radioaktiven Substanz grafisch wieder. Eingestellt werden können Zerfallskonstante und Anzahl der Iterationen, die aber auch manuell gesteuert werden können.
Hinweis: Diese Datei enthält Makros, die es gestatten, den Ausgangszustand wieder herzustellen und die Simulation über eine voreinstellbare Iterationsanzahl laufen zu lassen.
Zentrale Experimente Physik GOSt


Startseite → Ionisierende Strahlung radioaktiver Stoffe → Der radioaktive Zerfall als stochastischer Prozess - Tabellenkalkulation
Der radioaktive Zerfall als stochastischer Prozess - Tabellenkalkulation
Auf dieser Seite wird der Zerfall radioaktiver Substanzen mit Hilfe eines Tabellenkalkulationswerkzeugs modelliert. Beachten Sie dabei, dass es sich bei den dabei durchgeführten Rechnungen immer um diskrete Schritte handelt, dass also so getan wird, als würde während der jeweiligen Zeitschritte keinerlei Veränderung vorkommen und alle Veränderungen im Gleichtakt geschehen. In der Realität handelt es sich hingegen beim radioaktiven Zerfall sehr vieler Atome in seiner Gesamtheit und einen quasi-kontinuierlichen Prozess.
Bei dieser Art der Modellierung bedeut also die Zerfallswahrscheinlichkeit immer eine Wahrscheinlichkeit bezogen auf eine fiktive Zeitspanne, während die Zerfallswahrscheinlichkeit bzw. die Zerfallsrate bei einem natürlich ablaufenden Prozess mit der Einheit 1/s behaftet ist.
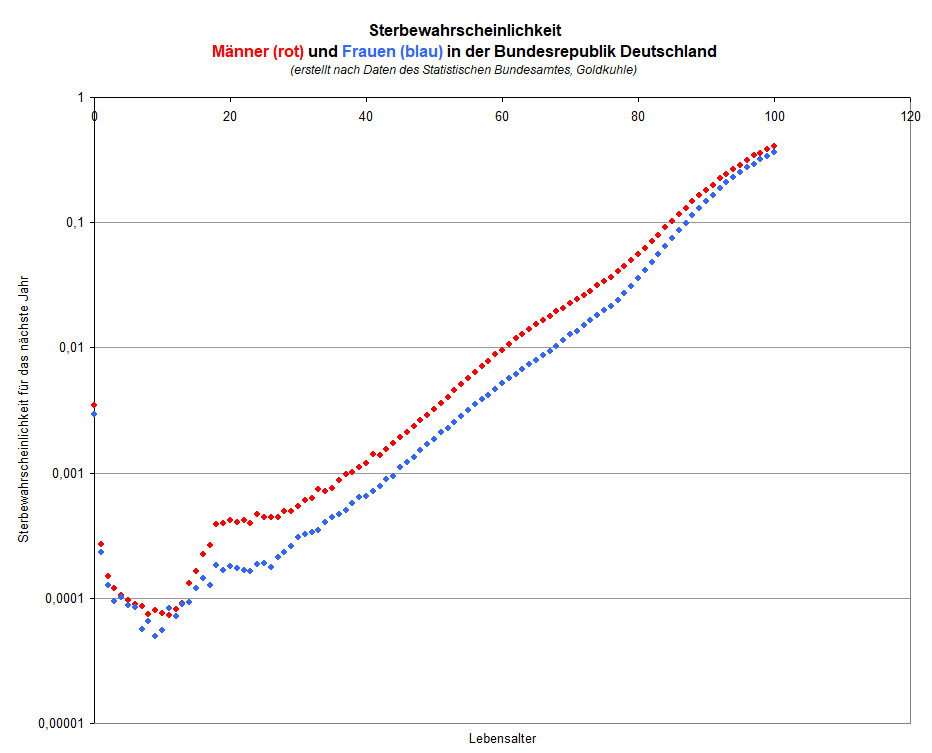
Vergleichen Sie die Sterbewahrscheinlichkeit bei Menschen in Abhängigkeit vom Lebensalter mit der Zerfallswahrscheinlichkeit radioaktiver Nuklide und nennen Sie den wesentlichen Unterschied im Verlauf der Kurven. Tragen Sie dazu in die Grafik für die o. g. Zerfallswahrscheinlichkeit $p=\frac{1}{10}$ eines radioaktiven Nuklids die entsprechende Kurve ein (Zeiteinheit 1 Jahr). Beachten Sie, dass die Hochachse logarithmisch skaliert ist.
Die Zerfallswahrscheinlichkeit betrage wieder $p=\frac{1}{10}=0,1$.
Berechnen Sie, wieviel Prozent der ursprünglichen Nuklidanzahl noch nach 10 Zeiteinheiten vorhanden sind, und vergleichen Sie Ihr Ergebnis mit der Simulation auf dem ersten Tabellenblatt "Zerfall Berechnung".
Tipp
Schauen Sie sich das zweite Tabellenblatt "Zerfallskurve linear" an. Notieren Sie für mindestens fünfmaliges Starten der Simulation den Durchschnittswert der aus der jeweils angegebenen Exponentialgleichung berechenbaren Halbwertszeit.
Das Absinken der Teilchenzahlen auf die Hälfte liegt für $p=\frac{1}{10}$, wie bei mehreren Simulationdurchläufen auf dem ersten Tabellenblatt "Zerfall Berechnung" in der Zeile 15 der angegebenen Teilchenzahlen erkennbar, i. d. R. zwischen der 5. und 7. Zeiteinheit.
Begründen Sie, dass beide Ergebnisse im Einklang stehen.
Tipp 1
Schauen Sie sich die zu zeigende Formel an. Die dort auftretenden Größen geben Ihnen einen Hinweis auf den Ansatz.
Stellen Sie einen Zusammenhang her zwischen der Wahrscheinlichkeit $p$ und der Zerfallskonstanten $\lambda$.
Der Zusammenhang zwischen der Zerfallskonstanten $\lambda$ und der Halbwertszeit $T_{1/2}$ liefert dann in Verbindung mit einer kurzen Rechnung die Begründung.
Beschreiben Sie das Prinzip, nach dem in den 50.000 Zellen des 1.000 mal 50 großen Felds jeweils entschieden wird, ob die betreffende Zelle unter Berücksichtigung der vorgegebenen Zerfallswahrscheinlichkeit jeweils grün oder weiß einzufärben ist.
Wählen Sie als Zerfallswahrscheinlichkeit zunächst den voreingestellten Werte für $p=\frac{1}{10}$.
Verfolgen Sie auf dem ersten Tabellenblatt "Zerfall Berechnung" der Datei für eines der 1000 Teilchen die
"Überlebenszeitspannen", wenn Sie die Simulation mehrfach hintereinander
ablaufen lassen (zur besseren Verfolgbarkeit ist das 10. Teilchen
dunkelgrün eingefärbt).
Nehmen Sie bewusst zur Kenntnis, wie stark bei jeder durchgeführten
Simulation die Überlebenszeitspannen der 1000 Teilchen variieren.
Wählen Sie auch andere Zerfallswahrscheinlichkeiten und beobachten Sie die Veränderungen.
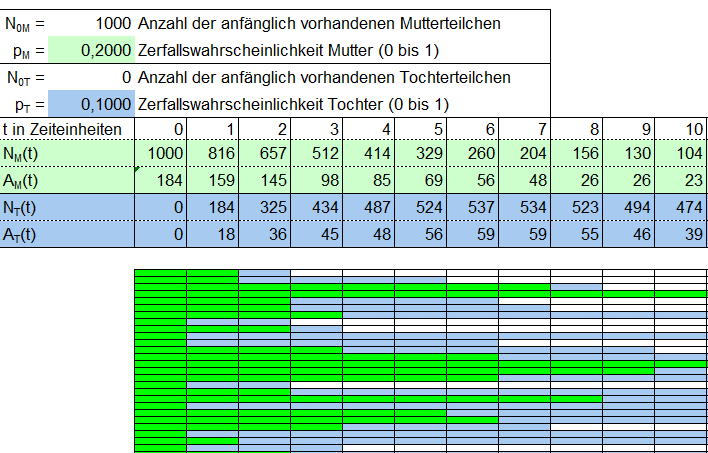
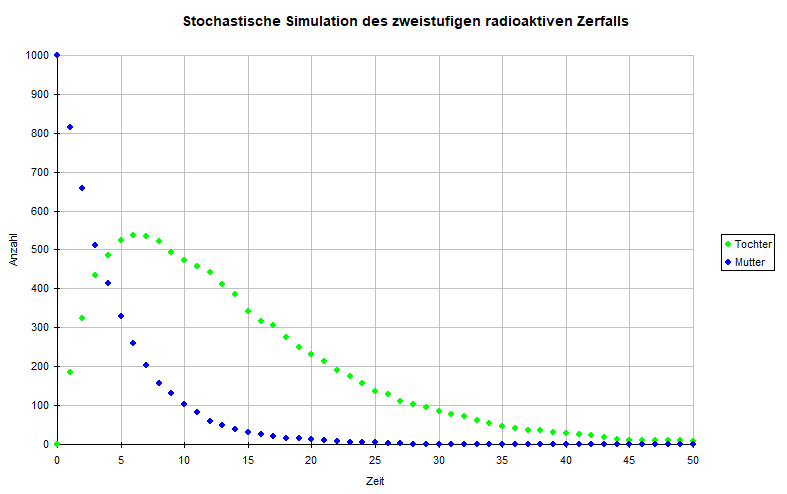
Die rechst stehende zweite Excel-Datei (bitte Hinweis zur Tabelle oben beachten) modelliert den zweistufigen Zerfallsprozess. Hier können Sie die Zerfallswahrscheinlichkeiten für die Mutter- sowie für die Tochtersubstanz wählen. Das erste Tabellenblatt zeigt durch farblich unterscheidbare Zellenfärbung die sich zufällig ergebende Lebensdauer der Mutter- und der Tochtersubtanz, auf dem zweiten Tabellenblatt werden die beiden Stoffmengen in einem Zeitdiagramm dargestellt.
- Beschreiben Sie den Einfluss des Verhältnisses beider Zerfallswahrscheinlichkeiten zueinander auf den Kurvenverlauf der Tochtersubstanz, indem Sie das sich Kurven anzeigen lassen für $\lambda_{Mutter}=2\cdot \lambda_{Tochter}$ und umgekehrt $\lambda_{Tochter}=2\cdot \lambda_{Mutter}$.
- Begründen Sie, ob in einem der beiden Fälle eine der beiden Kurven immer über bzw. unter der anderen liegt.
- Entscheiden Sie begründet, ob die Situation auftreten kann, dass nach einer gewissen Anlaufphase gleich viel Mutter- und Tochtersubstanz vorhanden sind, sodass beide Kurven dann nahezu aufeinander liegen.
- Treffen Sie eine analoge Entscheidung für die Gleichheit der Aktivitäten von Mutter- und Tochtersubstanz.
Tipp 1
Schauen Sie sich die zu zeigende Formel an. Die dort auftretenden Größen geben Ihnen einen Hinweis auf den Ansatz.
Tipp 1
Schauen Sie sich die zu zeigende Formel an. Die dort auftretenden Größen geben Ihnen einen Hinweis auf den Ansatz.
Mit Hilfe einer Tabellenkalkulation lässt sich der Zerfallsprozess anschaulich simulieren.
Laden Sie sich dazu diese Excel-Tabelle herunter und bearbeiten mit Hilfe des "Experimentierens" mit dieser Tabelle die folgenden Aufgaben.
Hinweis:
Das Tabellenblatt ist so eingestellt, dass eine (Neu-) Berechnung immer explizit gestartet werden muss. Sie können die Tabellenkalkulation direkt veranlassen, ein Rechnung zu starten, oder dafür auch die Schaltfläche verwenden.

Die Excel-Dateien wurden auf einem Windows-PC erstellt. Sie enthalten teilweise VBA-Makros und ActiveX-Steuerelemente. Daher sind sie ggf. nicht kompatibel mit Rechnern anderer Betriebssysteme und auch auf Tablets i. d. R. nicht lauffähig.
Die Excel-Dateien wurden auf einem Windows-PC erstellt. Sie enthalten teilweise VBA-Makros und ActiveX-Steuerelemente. Daher sind sie ggf. nicht kompatibel mit Rechnern anderer Betriebssysteme und auch auf Tablets i. d. R. nicht lauffähig.

Die Excel-Dateien wurden auf einem Windows-PC erstellt. Sie enthalten teilweise VBA-Makros und ActiveX-Steuerelemente. Daher sind sie ggf. nicht kompatibel mit Rechnern anderer Betriebssysteme und auch auf Tablets i. d. R. nicht lauffähig.