Zentrale Experimente Physik GOSt


Startseite → Elektronenbeugung → Voraussetzungen zur Theorie- und Experimententwicklung der Elektronenbeugung
Da man bereits entdeckt hatte, dass Licht unter bestimmten experimentellen Bedingungen nicht nur, wie bis um die Jahrhundertwende zum 20. Jahrhundert angenommen, Wellen- sondern auch Teilcheneigenschaften aufweisen kann, kam de Broglie Anfang der zwanziger Jahre des 20. Jahrhunderts auf die Idee, dass man auch den bis dahin ausschließlich mit Teilcheneigenschaften dargestellten Elektronen, wie allen Materieobjekten überhaupt, Welleneigenschaften zuweisen könnte.
De Broglie übertrug die Gleichung $\lambda=\frac{h}{p}$, die bis dahin nur für die sich mit Lichtgeschwindigkeit c ausbreitenden Photonen galt, "einfach" auf alle sich immer mit v < c bewegenden Materieobjekte, so auch auf Elektronen. Es sollte also für diese gelten: $\lambda=\frac{h}{m\cdot v}$. Er postulierte, dass man daher auch Elektronen eine Wellenlänge zuordnen könne, die gemäß dieser Gleichung von ihrer Masse und Geschwindigkeit abhängt.
Dafür gab es im Jahr 1924, bei der Veröffentlichung seiner Dissertation, jedoch noch keinerlei experimentelle Hinweise, sodass man erst gezielt Versuche entwickeln musste, die seine Angaben verifizieren konnten - wenn denn die de Broglie'sche Hypothese richtig war.
Diese Vorüberlegungen zeigen, dass man Gitter benötigt, wie man sie bei den inzwischen anhand der Röntgenstrukturanalyse bekannten Abständen von Kristallebenen findet. Würde man also analog zu den Interferenzerscheinungen mit Licht nun auch bei Elektronen Interferenzerscheinungen beobachten können, die zudem auch quantitativ mit der de Broglie'schen Gleichung verträglich sind, wäre de Broglies Hypothese verifiziert.
Daher wurden ab 1924 Experimente entwickelt, bei denen (im Wesentlichen nichtrelativistische) Elektronen auf Kristallgitter gelenkt wurden, mit dem Ergebnis, dass tatsächlich Interferenzerscheinungen auftraten und die Geometrie dieser Interferenzerscheinungen mit der de Broglie'schen Gleichung verträglich war - insbesondere auch für Elektronen unterschiedlicher Geschwindigkeiten.
Als Ersten gelangen Davisson und Germer - allerdings eher zufällig - solche (quantitativen) Interferenznachweise im Jahr 1927. Auf der folgenden Seite finden Sie einige Informationen zu ihrem Experiment, darüberhinaus auch hier eine Simulation und an dieser Stelle weitere Erklärungen.
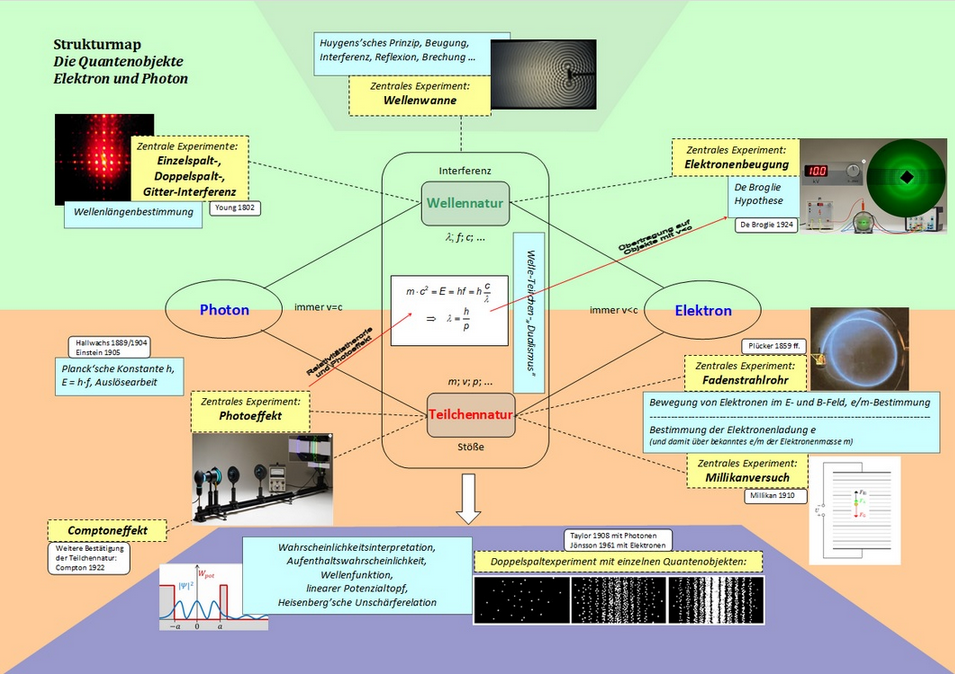
An dieser Stelle, die eine Seite im Rahmen des tetfolio-Kapitels "Photoeffekt" bildet, finden Sie eine zusammenfassende Übersicht (Strukturmap) über die grundlegenden Experimente sowie über die Sichtweisen hinsichtlich der Wellen- und Teilchenaspekte der Quantenobjekte Elektron und Photon.
Voraussetzungen zur Theorie- und Experimententwicklung der Elektronenbeugung
Anhand der Welleneigenschaften von Photonen wusste man bereits längere Zeit, dass Welleneigenschaften besonders dann gut beobachtet werden können, wenn man Licht auf Gitter fallen lässt, deren Gitterkonstanten in der Größenordnung der jeweiligen Wellenlänge liegt. Wollte man also Welleneigenschaften von Elektronen beobachten, musste man geeignete "Gitter" finden bzw. gezielt konstruieren, deren Gitterkonstante in der Größenordnung der postulierten Wellenlänge der verwendeten Elektronen lag.
Berechnen Sie die Wellenlänge nichtrelativistischer Elektronen gemäß der de Broglie'schen Gleichung, wenn die Elektronen mit einer Beschleunigungsspannung von U = 2 kV beschleunigt werden.
Nennen Sie dasjenige Phänomen bzw. denjenigen Effekt beim Licht, der - in genau umgekehrter Weise - nach seiner experimentellen Entdeckung erstmalig mithilfe von Teilchenaspekten theoretisch erklärt werden konnte.
Leiten Sie, ausgehend von der für die Photonen geltende Gleichung $E=h\cdot f$, die Gleichung $\lambda=\frac{h}{p}$ unter Verwendung der relativistischen Beziehung $E=m\cdot c²$ zwischen Energie und Masse her.
$E=\frac{1}{2}\cdot m\cdot v²$
Tipp
Ergebnis